Limites de contrôle vs de tolérance : connaissez-vous la différence?
Rédigé par Vincent Béchard et Martin Carignan le 2025-10-16
Lisez-moi! Je ne suis pas (tant que ça) statistique!
Pourquoi des limites en statistique?

Un peu de philosophie autour des différentes définitions des limites en statistique… La plus courante est probablement l'intervalle de confiance sur la moyenne (plage de valeurs dans laquelle la moyenne réelle de la population devrait se situer avec un niveau de confiance donné). Viennent ensuite les limites de spécification (limites inférieure et supérieure définissant ce qui est acceptable du point de vue du client). Mais il existe également les limites de la carte de contrôle (variabilité attendue à partir des données historiques du processus). Et oui, nous ajoutons maintenant un quatrième type : les limites de tolérance (variabilité inférée de la population à partir d'un échantillon).
Pourquoi tant de types différents de limites? Parce que les limites doivent être adaptées à l'objectif du processus décisionnel basé sur les données :
- Intervalle de confiance sur la moyenne : pour déterminer si l’échantillon fournit une précision suffisante sur la moyenne estimée de la population ou pour tester l’hypothèse « La moyenne de la population est-elle différente de la cible? »; calculé à partir des données de l’échantillon, sa largeur diminue à mesure que la taille de l’échantillon augmente.
- Limites de spécification : données ou imposées par le client pour distinguer un bon produit d’un mauvais; vous pouvez les contester ou remettre en question la méthodologie utilisée pour les établir, mais elles resteront des valeurs imposées indépendamment des données historiques.
- Limites de la carte de contrôle : pour déterminer si le processus est stable et sous contrôle; calculées à partir des données historiques. Leur calcul n’est pas affecté par la taille de l’échantillon, bien qu’un plus grand nombre de données augmente la précision du calcul.
- Limites de tolérance : nous les définirons dans la section suivante.
Pour obtenir la plage potentielle des valeurs individuelles attendues de leur procédé, certains utilisent les limites de contrôle d'une carte de contrôle I-MR. Cependant, ce n'est peut-être pas la meilleure approche. Il semble donc nécessaire de mieux comprendre la différence entre limites de contrôle et limites de tolérance!
REMARQUE : l'intervalle de confiance sur la moyenne est le seul type, parmi ceux mentionnés ci-dessus, qui ne traite pas de la largeur de distribution des valeurs individuelles; il se concentre uniquement sur la question de savoir où se situe la moyenne de la population.
Limites de contrôle et de tolérance expliquées
Les deux types de limites visent à déterminer une plage qui reflète la variabilité intrinsèque des données. Elles reposent toutes deux sur la notion de « sigma », une mesure de la variabilité :
Limites de contrôle
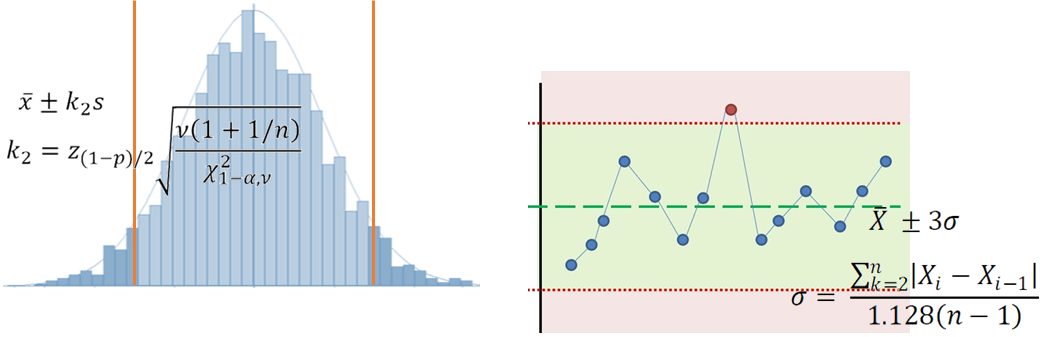
Le sigma (σ) représente la variation naturelle du processus. Pour les valeurs individuelles, σ est obtenu à partir de la variation moyenne point-à-point de la série chronologique (appelée étendue mobile). Important : les données doivent être organisées par ordre chronologique! Les limites sont obtenues en prenant la moyenne ± 3σ. La constante (3) n’est pas affectée par la taille de l’échantillon utilisé pour calculer les limites. Cela revient à supposer que σ (calculé à partir des données) est en fait le σ de la population!Voir les détails statistiques.

Limites de tolérance
Le sigma (σ) représente la variation de la population étudiée. Il est estimé à partir de l'écart-type des données de l'échantillon. Les limites représentent l'intervalle devant couvrir au moins un pourcentage donné de la population avec un niveau de confiance donné. Il s'agit d'une inférence des données de l'échantillon à la population sous-jacente (inconnue). On suppose que les données suivent une distribution Normale.Voir les détails statistiques.
Où voit-on habituellement ces limites? Les limites de contrôle apparaissent sur les cartes de contrôle, tandis que les limites de tolérance apparaissent sur les histogrammes! Les limites de contrôle servent à détecter les variations d'un procédé dans le temps, tandis que les limites de tolérance définissent la plage couvrant un pourcentage de la population (en supposant que les données échantillonnées soient représentatives de la population).
Illustration du concept de limites de tolérance
Un nouveau produit est en cours de fabrication sur une machine. L'ingénieur de procédé souhaite évaluer la probabilité qu'une spécification de qualité soit respectée (la largeur de cette spécification est de 60). Idéalement, le procédé devrait produire au moins 99,73% de produits conformes. Afin d'obtenir rapidement une réponse, il conçoit une expérience où il fait varier tous les facteurs majeurs susceptibles de contribuer à la variabilité de la qualité du produit. Il collecte 25 observations qui devraient représenter la variation normale attendue de ce produit pour les productions futures. L'écart-type de ces 25 observations est de 10.
Situation #1: Il utilise des limites de contrôle (±3σ) pour évaluer la variation attendue de ce produit (en supposant que ces limites couvrent 99,73% de la population si elle est distribuée normalement). Il obtient la largeur de limite suivante : ±3*10 = 60. Il conclut que 99,73% des futurs produits devraient respecter les limites de la spécification. C'est un succès!!! Vraiment?
Situation #2:Il utilise un calcul d’intervalle de tolérance pour évaluer la variation attendue de ce produit. L’intervalle calculé doit contenir au moins 99,73% des résultats de la population avec un niveau de confiance de 95%. Il obtient la largeur des limites suivante : ±4,04*10 = 80,8. Il réalise qu’avec la taille réelle de l’échantillon, il est impossible de conclure que nous avons la capacité attendue à respecter les limites de spécification. Deux possibilités s’offrent alors à lui :
- Recueillir un total d’environ 400 observations et espérer que l’écart-type observé soit inférieur ou égal à 10. En effet, avec 400 observations, la valeur de la constante chute à 3,19.
- Réellement travailler sur les causes racines : éliminer les sources de variabilité du procédé et réévaluer le nouvel écart-type
Le danger d’utiliser systématiquement ±3σ pour estimer les limites de tolérance
Comparons la probabilité de couvrir au moins 99,73% des données avec un intervalle obtenu en utilisant ±3σ. Pour un échantillon de 25 observations, cette probabilité n'est que de 59% !!!
L'hypothèse de couverture de 99,73 % des limites de ±3σ n'est valable que… lorsque la taille de l'échantillon est très importante! Avec moins de 50 observations, la probabilité que les limites de contrôle couvrent réellement 99,73% de la population est inférieure à 70%. Si la question est : « Quelle est la plage de valeurs attendue? » et que le nombre d'observations disponibles est limité, les limites de tolérance sont alors plus utiles que les limites des cartes de contrôle!
En conclusion
En statistique, les limites de contrôle et de tolérance sont toutes deux importantes. Néanmoins, il est crucial de comprendre leur fonction et les hypothèses qui les sous-tendent. Les deux types de limites supposent des données distribuées normalement. En revanche, les limites des cartes de contrôle reposent sur des observations ordonnées dans le temps et supposent que le sigma à court terme est représentatif de la variation « normale » du processus. L'objectif de ces limites est de faire le suivi d’un processus afin d'identifier les causes de variation assignables.
À l'inverse, les limites de tolérance traitent des données échantillonnées et permettent à l'analyste de contrôler la couverture de la distribution et le niveau de confiance. Elles permettent d'identifier la plage de valeurs qui couvrira un pourcentage déterminé de la population à un niveau de confiance donné. Puisqu'elles considèrent l'incertitude relative à la taille de l'échantillon, elles sont très utiles lorsque la quantité de données disponibles est limitée.
Vous désirez en savoir plus?
Toutes les analyses présentées dans cet article ont été réalisées avec notre complément Excel pour l’analyse statistique; visitez cette page pour découvrir ses fonctionnalités. Chez Différence, notre expertise est axée sur la statistique et la science des données, les applications du Lean et l'Excellence opérationnelle, ainsi que sur la simulation. N'hésitez pas à demander plus d'information en nous contactant.

