Optimization and machine learning altogheter???
Modern data science techniques opened new ways to perform process optimization. It is very tempting to seek for highly desirable conditions straight from the data without having to develop complex simulations. The information is there, sitting in the data table, just waiting to be extracted... Why not "simply" develop machine learning applications to crawl and fit the data? We developed an approach for automatically building models from the data, followed by a run of black-box optimization. In a nutshell, the steps are:
- Normalize the data and use clustering to discover where the data is spreading in space
- Use predictive modelling to capture the relationship between controllable/actionable parameters and performance criterion (random forests is used by default)
- Setup a Monte-Carlo simulation sandbox: variability around every trial point is evaluated to estimate pointwise robustness (insensitivity to local perturbations)
- Trigger the optimizer: repeatedly try new points to improve the performance criterion value until optimizer concludes to optimality
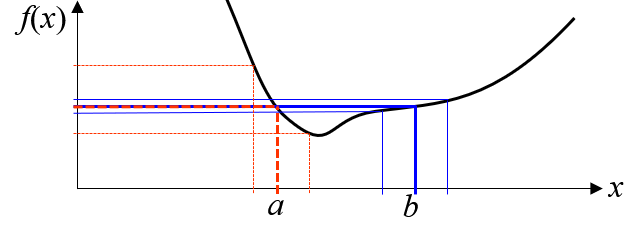
A trial point is considered “better” than others if it is close enough to historical data and its predicted value is lower or higher (minimizing or maximizing) than the best so far. But! A compromise is accepted for exceptionally robust points: small degradations in performance in exchange of significant gain in robustness. This tradeoff is illustrated below: points a) and b) have the same value, but point b) is more interesting because it reduces the output variability.
Complex optimization problem looking for data!
The resulting optimization problem is difficult since gradient may not be defined, data can have subgroups (disjoint domain), the relationship can be non-smooth and noisy. Research and experience lead to recommending the MADS algorithm (mesh adaptive direct searches), a powerful contemporary algorithm (see great description here).
This data-driven optimization approach requires... data! When there are at least 20 observations per variable, it gives very interesting results. For 10 parameters to tune simultaneously, at least 150 to 200 observations will be sufficient. For bigger datasets, the embedded clustering and predictive modelling will handle size so that the optimizer will remain lightning fast.
A short example using open-source data
We reused an open-source machine learning dataset on concrete properties. The goal is to determine the mixing recipe and preparation rules that will robustly maximize concrete strength. It is small dataset (1030 observations, 9 variables), but it is challenging for optimizers and very useful to illustrate the behavior of our robust data-driven approach.
This first figure compares 3 direct search derivative-free optimization algorithms. Because of the difficult tradeoff between performance and robustness in this problem, only MADS successfully increased concrete resistance. The underlying Monte-Carlo simulation showed that variability was decreased by a factor of 3!

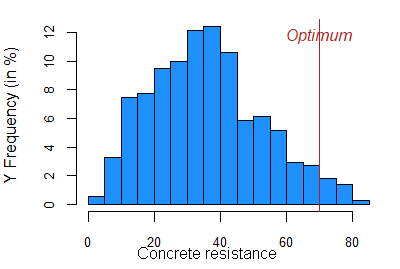
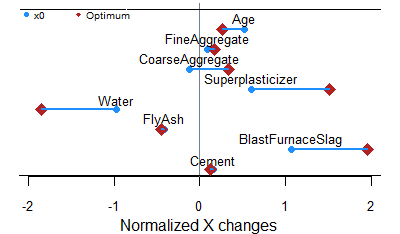
Perfect match between optimization and machine learning!
This framework, including the MADS algorithm was implemented in R, a powerful mathematical programming language. Machine learning is a powerful automated way to discover the data domain and to predict process performance. Monte-Carlo simulation is a simple tool to evaluate pointwise robustness to local perturbations. Black-box optimization, more specifically the MADS algorithm, can truly optimize the resulting problem. And there is a robust optimum obtained directly from the data... Data science can be so exciting!
Want to learn more?
At Différence, our core expertise is centered on statistic and data science, Lean applications and operational excellence, and... simulation! We can train, coach and help practitioners to learn how to use optimization! and Discrete Event Simulation. Don’t hesitate to ask for more information by contacting us.


